The identity function on A is iA:A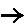 A where iA(a)=a for each a
A where iA(a)=a for each a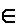 A. This is a one-to-one correspondence and so is invertible. It is, in fact, its own inverse.
A. This is a one-to-one correspondence and so is invertible. It is, in fact, its own inverse.
The function f:Z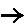 Z such that f(a)=a−4 for each a
Z such that f(a)=a−4 for each a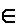 Z is a one-to-one correspondence and f −1(a)=a+4.
Z is a one-to-one correspondence and f −1(a)=a+4.