Partial Orders

A relation R on a set S is a partial ordering or partial order if it is reflexive, antisymmetric and transitive. A set S together with a partial order R is called a partially ordered set or poset and is denoted (S,R).

For example, the relation "less than or equal to" is a partial ordering on the integers. In this case (a,b) 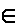R if a ≤ b.

a ≤ a so R is reflexive.
a ≤ b implies that b ≤ a only when a = b so R is antisymmetric.
if a ≤ b and b ≤ c then a ≤ c so R is transitive.

So (Z, ≤) is a poset.